ഫ്ലാഷിലെ ആനിമേഷനുകള്‍ (ഭാഗം രണ്ട്)
അഡോബി ഫ്ലാഷില്‍ സാധ്യമാവുന്ന മോഷന്‍ ട്വീനിംഗിനെക്കുറിച്ചും, മോഷന്‍ ട്വീനിംഗിലെ വിവിധ സാധ്യതകളെക്കുറിച്ചും നാം കഴിഞ്ഞ ഭാഗത്തില്‍ മനസിലാക്കിയല്ലോ? ഫ്ലാഷില്‍ ലഭ്യമായ മറ്റൊരു ആനിമേഷന്‍ സങ്കേതമായ ഷേപ്പ് ട്വീനിംഗിനെക്കുറിച്ചാണ് ഈ ഭാഗത്തില്‍ പ്രതിപാദിക്കുന്നത്. മോഷന്‍ ട്വീനിംഗ് ഉപയോഗിച്ച് ലൈബ്രറിയില്‍ ലഭ്യമായ ഒരു സിംബലിനെയാണ് നാം ആനിമേറ്റ് ചെയ്തത്. ഓബ്ജക്ടിന്റെ അടിസ്ഥാന രൂപത്തില്‍ മാറ്റം വരുത്താതെയുള്ള ആനിമേഷനുകളായിരുന്നു മോഷന്‍ ട്വീനിംഗില്‍ സാധ്യമായത്. എന്നാലിവിടെ വസ്തുവിന്റെ അടിസ്ഥാനരൂപത്തിലാണ് നാം മാറ്റം വരുത്തുന്നത്. അതായത് ഫ്ലാഷില്‍ ലഭ്യമായിരിക്കുന്ന ഫില്‍/സ്ട്രോക്ക് കളറുകള്‍ ഉപയോഗിക്കുന്ന വസ്തുക്കളില്‍ മാത്രമാണ് ഷേപ്പ് ട്വീനിംഗ് നമുക്ക് ഉപയോഗിക്കുവാന്‍ സാധിക്കുക. ഒരു ഷേപ്പ് ട്വീനിംഗ് ചെയ്തു നോക്കി നമുക്ക് ഇതിനെക്കുറിച്ച് കൂടുതലായി മനസിലാക്കാം.
ഒരു പുതിയ ഫ്ലാഷ് ഫയല്‍ തുറന്ന്, ലഭ്യമായിരിക്കുന്ന ലെയ‌റില്‍ ഒന്നാമത്തെ ഫ്രയിമില്‍ ചിത്രത്തില്‍ കാണുന്ന രീതിയില്‍ ഒരു സമചതുരം വരയ്ക്കുക. സമചരുതത്തിന്റെ ഫില്‍ കളറായ നീലയും, സ്ട്രോക്ക് കളറായി വെളുപ്പും സെലക്ട് ചെയ്തിരിക്കുന്നു. അതേ ലെയ‌റില്‍ അന്‍പതാമത്തെ ഫ്രയിമില്‍ മറ്റൊരു പുതിയ കീഫ്രയിം (ബ്ലാങ്ക് കീഫ്രയിം) കൂട്ടിച്ചേര്‍ത്ത്, അവിടെ ചിത്രത്തില്‍ കാണുന്ന രീതിയില്‍ ഒരു തൃകോണവും വരയ്ക്കുക. തൃകോണത്തിന്റെ ഫില്‍ കളറായി ചുവപ്പും, സ്ട്രോക്ക് കളറായി കറുപ്പും സെലക്ട് ചെയ്യുക.
സമചതുരം സ്റ്റേജില്‍ ഇടതുവശത്തോടു ചേര്‍ന്നും തൃകോണം വലതുവശത്തോടു ചേര്‍ന്നും ക്രമീകരിക്കുക. സമചതുരം വരച്ചിരിക്കുന്ന ഫ്രയിമില്‍ (ഫ്രയിം: 1) വലതുമൌസ് ബട്ടണ്‍ അമര്‍ത്തി, തുറന്നുവരുന്ന മെനുവില്‍ നിന്നും Create Shape Tween എന്ന ഓപ്ഷന്‍ സെലക്ട് ചെയ്യുക. മുകളിലെ ചിത്രത്തില്‍ കാണുന്ന രീതിയില്‍ രണ്ട് കീഫ്രയിമുകള്‍ക്കും ഇടയിലുള്ള ഫ്രയിമുകള്‍ ഇളം‌മഞ്ഞ നിറത്തിലാവുകയും, രണ്ടു ഫ്രയിമുകളും ഒരു ആരോ ഉപയോഗിച്ച് ബന്ധിക്കപ്പെട്ടിരിക്കുകയും ചെയ്യും. ഡോട്ടഡ് ലൈനുപയോഗിച്ചാണ് ഇവരണ്ടും ബന്ധിപ്പിച്ചിരിക്കുന്നതെങ്കില്‍, അതിനര്‍ത്ഥം ആനിമേഷന്‍ ശരിയായല്ല നല്‍കിയിരിക്കുന്നതെന്നാണ്. ഏതെങ്കിലുമൊരു കീഫ്രയിമില്‍, ഫില്‍/സ്ട്രോക്ക് കളറല്ലാതെ മറ്റൊരു ഓബ്ജക്ട് അടങ്ങിയിരിക്കുമ്പോഴാണ് ഈ പ്രശ്നം ഉണ്ടാവുക. ശരിയായി ഓബ്ജക്ടുകള്‍ രണ്ട് കീഫ്രയിമുകളും നല്‍കിയിട്ടുണ്ടെങ്കില്‍ ലഭ്യമാവുന്ന ആനിമേഷനാണ് താഴെ കാണുന്നത്.
ചിത്രത്തിന്റെ രൂപവും നിറവും ക്രമമായി വ്യത്യാസപ്പെടുന്ന ഒരു ആനിമേഷനാണ് നമുക്കിപ്പോള്‍ ലഭിച്ചത്. Ctrl + Enter അമര്‍ത്തി നമുക്ക് ഈ ആനിമേഷന്‍ പ്രിവ്യൂ കാണാവുന്നതാണ്. സമചതുരത്തിന്റെ സ്ഥാനത്ത് ഇംഗ്ലീഷ് ലെറ്റര്‍ N-ഉം, തൃകോണത്തിന്റെ സ്ഥാനത്ത് Z-ഉം വരച്ച് ഇതേ ആനിമേഷന്‍ ഒന്നുകൂടി ചെയ്തു നോക്കാം. 
ടെക്സ്റ്റ് ടൂള്‍ സെലക്ട് ചെയ്ത്, സ്റ്റാറ്റിക്ക് ടെക്സ്റ്റായി ഇമ്പാക്ട് ഫോണ്ട് ഉപയോഗിച്ച് ഈ അക്ഷരങ്ങള്‍ ടൈപ്പ് ചെയ്ത ശേഷം, ബ്രേക്ക് (Ctrl + B) ചെയ്താല്‍ മതിയാവും. ഇപ്പോള്‍ ഒരു ഫില്‍ ഓബ്ജക്ടായി അക്ഷരങ്ങള്‍ നമുക്ക് ലഭ്യമാവും. ആവശ്യമുള്ള സ്ട്രോക്ക് കളര്‍ ഇങ്ക്-ബോട്ടില്‍ ടൂള്‍ ഉപയോഗിച്ച് നല്‍കാവുന്നതാണ്. ചിത്രത്തില്‍ കാണുന്ന N, Z എന്നിവ ഒന്നാമത്തേയും അന്‍പതാമത്തേയും ഫ്രയിമില്‍, രണ്ടു വശങ്ങളിലായി ക്രമീകരിക്കുക. ഷേപ്പ് ട്വീനിംഗ് പ്രയോഗിക്കുമ്പോള്‍ താഴെക്കാണുന്ന രീതിയിലൊരു ആനിമേഷനാവും നമുക്ക് ലഭിക്കുക.
ഷേപ്പ് ഹിന്റുകള്‍
മുകളില്‍ വിവരിച്ച ആനിമേഷനില്‍; N, Z എന്നീ അക്ഷരങ്ങള്‍ക്ക് ലഭ്യമായ മൂലകള്‍ തുല്യമാണെങ്കിലും, ഫ്ലാഷ് സ്വന്തം ഇഷ്ടപ്രകാരമാണ് ഷേപ്പ് ട്വീനിംഗ് സാധ്യമാക്കിയിരിക്കുന്നത്. N എന്ന അക്ഷരത്തിന്റെ മൂലകള്‍ തന്നെ Z എന്നതിന്റേയും മൂലകളായി മാറണമെങ്കില്‍, അത് നാം പ്രത്യേകം ഫ്ലാഷിനോട് നിര്‍ദ്ദേശിക്കണം. അതിനായി ഉപയോഗിക്കുന്ന സങ്കേതമാണ് ഷേപ്പ് ഹിന്റുകള്‍. ആദ്യമായി ഒന്നാമത്തെ ഫ്രയിമില്‍ ആവശ്യമുള്ള ഷേപ്പ് ഹിന്റുകള്‍ ചേര്‍ത്ത്, അവ N എന്ന അക്ഷരത്തിന്റെ മൂലകളില്‍ ക്രമീകരിക്കണം. Ctrl + Shift + H അമര്‍ത്തിയോ, പ്രധാനമെനുവില്‍ Modify > Shape > Add Shape Hint സെലക്ട് ചെയ്തോ ഷേപ്പ് ഹിന്റുകള്‍ സ്റ്റേജിലേക്ക് ചേര്‍ക്കാവുന്നതാണ്. ഒരു ചെറിയ വൃത്തത്തിനുള്ളില്‍ a, b, c എന്നിങ്ങനെയാവും ഷേപ്പ് ഹിന്റുകള്‍ അടയാളപ്പെടുത്തിയിരിക്കുക. ആദ്യം സ്റ്റേജിലേക്ക് ചേര്‍ക്കുമ്പോള്‍ വൃത്തത്തിന്റെ നിറം ചുവപ്പായിരിക്കും. ചിത്രം ശ്രദ്ധിക്കുക. ഷേപ്പ് ഹിന്റിനു മുകളില്‍ ക്ലിക്ക് ചെയ്ത് ഡ്രാഗ് ചെയ്ത്, അതിന്റെ സ്ഥാനം ക്രമീകരിക്കാവുന്നതാണ്. കൂടുതല്‍ ഷേപ്പ് ഹിന്റുകള്‍ ഈ രീതിയില്‍ മൂലകളില്‍ (N) ക്രമീകരിക്കുക.
തുടര്‍ന്ന് അന്‍പതാമത്തെ ഫ്രയിമിലെത്തുക. അവിടെയും ഇത്രയും തന്നെ ഷേപ്പ് ഹിന്റുകള്‍ സ്റ്റേജിലേക്ക് കൂട്ടിച്ചേര്‍ക്കപ്പെട്ടിരിക്കും. അവിടെയും ഷേപ്പ് ഹിന്റുകളുടെ സ്ഥാനം ആവശ്യാനുസരണം ക്രമീകരിക്കുക. ശരിയായി ക്രമീകരിച്ചു കഴിഞ്ഞാല്‍, ആദ്യ ഫ്രയിമിലെ ഷേപ്പ് ഹിന്റുകള്‍ ഇളം‌മഞ്ഞ നിറത്തിലും, അവസാന ഫ്രയിമിലെ ഷേപ്പ് ഹിന്റുകള്‍ ഇളം‌പച്ച നിറത്തിലും കാണപ്പെടും. അടുത്ത ചിത്രം കാണുക.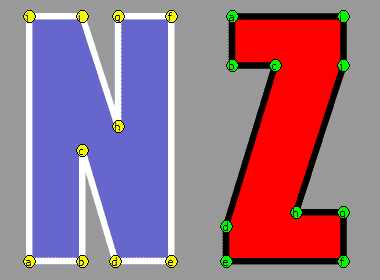
ഷേപ്പ് ഹിന്റുകള്‍ ഉപയോഗിച്ചും, ഉപയോഗിക്കാതെയും ഇതേ ആനിമേഷന്‍ ചെയ്യുമ്പോഴുള്ള വ്യത്യാസം അടുത്ത ചിത്രത്തില്‍ നിന്നും മനസിലാക്കുവാന്‍ സാധിക്കും. Ctrl + Alt + H അമര്‍ത്തി ഷേപ്പ് ഹിന്റ് സ്റ്റേജില്‍ ദൃശ്യമാക്കുകയോ അദൃശ്യമാക്കുകയോ ചെയ്യാവുന്നതാണ്. ഏതെങ്കിലുമൊരു ഷേപ്പ് ഹിന്റിനു മുകളില്‍ വലതുമൌസ് ബട്ടണ്‍ അമര്‍ത്തിയാല്‍, ഷേപ്പ് ഹിന്റുകള്‍ ഓരോന്നായോ മുഴുവനായോ ഒഴിവാക്കുവാനുള്ള ഓപ്ഷനുകള്‍ ലഭിക്കുന്നതാണ്. മോഷന്‍ ട്വീനിംഗില്‍ പരിചയപ്പെട്ട ഈസ് ഇന്‍/ഔട്ട് സാധ്യതകള്‍ ഷേപ്പ് ട്വീനിംഗിലും ഉപയോഗിക്കാവുന്നതാണ്. ഹിന്റുകള്‍ രണ്ട് ഫ്രയിമിലും പ്ലോട്ട് ചെയ്യുന്നതിന് അനുസൃതമായി ആനിമേഷനിലും മാറ്റമുണ്ടാവും.
(2007 ഡിസംബര്‍ ലക്കം ഇന്‍ഫോകൈരളി കമ്പ്യൂട്ടര്‍ മാഗസീനില്‍ പ്രസിദ്ധീകരിച്ചത്.)
Keywords: Adobe, Flash, Animation, Tutorial, Malayalam, Motion, Shape, Shape Hints, Tween, Macromedia, InfoKairali
--
12 comments:
ഫ്ലാഷിലെ മോഷന്‍ ട്വീന്‍ ആനിമേഷനെക്കുറിച്ച് കഴിഞ്ഞ പോസ്റ്റില്‍ വിവരിച്ചിരുന്നുവല്ലോ? മറ്റൊരു സാധ്യതയായ ഷേപ്പ് ട്വീന്‍ ആനിമേഷനെക്കുറിച്ചാണ് ഇവിടെ.
--
ഈ ബ്ലോഗില്‍ പ്രദിപാതിച്ചിരിക്കുന്നതൊക്കെ കമ്പ്യൂട്ടറിന്‍‌റ്റെ ഒരു തലത്തിലുള്ള ഉപയോഗം മാത്രമല്ലെ ആവുന്നുള്ളു പിന്നെ എങ്ങിനെയാണ് കമ്പൂട്ടറിനെക്കുറിച്ചുള്ള എന്തും ഏതും എന്ന് പറയാന്‍ പറ്റുക?
കമ്പ്യൂട്ടറുമായി ബന്ധപ്പെട്ട (എനിക്കറിയാവുന്ന) എന്തും ഏതും... എന്നല്ലേ അര്‍ത്ഥമാക്കേണ്ടത്? കമ്പ്യൂട്ടറുമായി ബന്ധപ്പെട്ട് എനിക്കറിയാവുന്ന എന്തുകാര്യങ്ങളും ഏതുകാര്യങ്ങളും എഴുതിവെയ്ക്കുവാനൊരിടം, അത്രയുമേ ഉദ്ദേശിച്ചുള്ളൂ... ഇതിനത്രയ്ക്ക് പ്രാധാന്യമുണ്ടോ! രണ്ടിടത്ത് കമന്റ് കണ്ടതുകൊണ്ട് ചോദിച്ചതാണ്‍!!!
:)
--
ടാഗ് ലൈന്‍ കണ്ടപ്പോള്‍ ചോദിച്ചുപോയതാണ് ;)കമ്പൂട്ടര്‍ എങ്ങിനെയാണ് കണക്ക് കൂട്ടുന്നതെന്നൊന്ന് പറഞ്ഞു തരാമോ ? അഞ്ച് + ആറ് = പതിനൊന്ന് ഇതെങ്ങിനെയാണ് ഒരു കമ്പൂട്ടര്‍ ചെയ്യുന്നത് ? ഇതെങ്ങിനെയാണ് ഒരു കമ്പൂട്ടറില്‍ ( കാല്‍കുലേറ്ററില്‍ ) നടക്കുന്നത്
Enthupatti Hari?
I am waiting for your answer?
ബെസ്റ്റ് കണ്ണാ ബെസ്റ്റ്.... ടാഗ് ലൈന്‍ വായിച്ചാല്‍ കമ്പ്യൂട്ടറുമായി ബന്ധപ്പെട്ട എന്ത് വേണേലും എഴുതും എന്നല്ലേ സഹ്യാ മീനിങ്ങ്? ഞാന്‍ പറഞ്ഞാല്‍ മതിയോ സഹ്യാ ഉത്തരം?
അല്ലേല്‍ വേണ്ട... ഇവിടെയെങ്ങാന്‍ പോയി നോക്കന്നേ..
vishNu - aRiyaaththa kaaryangngaLekkuRichchu aRiyillenkil paRayaruth , avide enthaaNezhuthiyirikkunnathennnu vaayichchu manassilaaakkuka aadyam ennittu mathi ii supporting :
avite paranjnjirikkunnath computer arithematic anishTaa , athaayath decimal to analog conversion , arithematic logic operation etc athaano ente chodyam?
aadyam chodyam manassilaakki ennitt mathi uththaram
വിഷ്ണു ,കൂട്ടുകാര്‍ക്ക് കിട്ടിയാല്‍ താങ്ങാന്‍ വന്നതാകും അല്ലെ? താനൊക്കെയാണ് ബൂലോഗത്തിലുണ്ടായിരുന്ന ഹാര്‍മണി നശിപ്പിച്ചത്. തനിക്കെന്റെ ചോദ്യത്തിനുത്തരം പറയാനറിയുമെങ്കില്‍ പറയുക ഇല്ലെങ്കില്‍ പോയി രണ്ട് ഒലിപ്പീരന്‍ കവിത എഴുതാന്‍ നോക്ക്.
@ സഹ്യന്‍,
ഉത്തരം പറയാഞ്ഞതിനുള്ള കാരണങ്ങള്‍:
• കാര്യമായുള്ള ചോദ്യമാണിതെന്നു കരുതുന്നില്ല. (അവസാനം വിഷ്ണുവിനോട് പറഞ്ഞത് ‘കൂട്ടുകാര്‍ക്ക് കിട്ടിയാല്‍ താങ്ങാന്‍ വന്നതാവും’ എന്നതില്‍ നിന്നും, എനിക്കിട്ടൊന്ന് കൊട്ടിയതാണെന്ന് വ്യക്തം. :D) കമ്പ്യൂട്ടറിനെക്കുറിച്ചുള്ള അഖിലവിജ്ഞാനകോശമാണ് ഞാനെന്ന അര്‍ത്ഥത്തിലല്ല ആ ടാഗ് എഴുതിയത്. എനിക്കറിയാവുന്ന കാര്യങ്ങള്‍ പങ്കുവെയ്ക്കുന്നു എന്നുമാത്രം.
• ഇനി കാര്യമായുള്ള ചോദ്യമായിരുന്നെങ്കില്‍, സഹ്യന്‍ എന്താവും ചെയ്തിരിക്കുക? ഇവിടെ ചോദിച്ചു കാത്തു നില്‍ക്കാതെ, മറ്റു മാര്‍ഗങ്ങളിലൂടെ ഉത്തരം കണ്ടെത്തുമായിരുന്നു, ഒരുപക്ഷെ സമയം പോലെ ഇവിടെ അതു പങ്കുവെയ്ക്കുമായിരുന്നു; ശരിയല്ലേ?
• പോസ്റ്റിന്റെ പരിധിക്കുവരുന്ന ഒരു സംശയമായി തോന്നിയില്ല.
• ഇങ്ങിനെയുള്ള ചോദ്യങ്ങള്‍ക്ക് ഉത്തരം പറയുക അത്ര എളുപ്പവുമല്ല. ഉദാ: ഒരു അമ്മൂമ്മ ചോദിക്കുകയാണ്, “മോനേ, ഈ കമ്പ്യൂട്ടറെങ്ങിനെയാ രണ്ട് അക്കങ്ങള്‍ കൂട്ടിത്തരുന്നത്?” എന്നു ചോദിക്കുമ്പോള്‍ നല്‍കുന്ന ഉത്തരവും; ഒരു +2വിനു പഠിക്കുന്ന കുട്ടിക്കു നല്‍കുന്ന ഉത്തരവും; ഒരു എം.സി.എ. വിദ്യാര്‍ത്ഥിക്കു നല്‍കുന്ന ഉത്തരവും വ്യത്യസ്തമായിരിക്കും. അല്ലേ? സഹ്യന്‍ ഏതുവിഭാഗത്തില്‍ വരുന്നു എന്ന് അറിയില്ല!
• വളരെ ആധികാരികമായി, വിശദീകരിച്ച് ഒരു ഉത്തരം നല്‍കുവാനുള്ള അറിവ് എനിക്കില്ല.
അതുകൊണ്ട് എനിക്കറിയാവുന്ന ചെറിയ കാര്യങ്ങള്‍ പങ്കുവെച്ച് ഞാന്‍ തുടരട്ടെ... :) <-- സ്മൈലി
@ വിഷ്ണു,
:)
കമ്പ്യൂട്ടറുകള്‍ക്ക് ആകെ മനസിലാവുന്നത് 1, 0 എന്നീ വിലകളാണ്. അതിനാല്‍ നമ്മള്‍ നല്‍കുന്ന ഡെസിമല്‍ വിലകളെ ബൈനറി രൂപത്തിലാണ് കമ്പ്യൂട്ടര്‍ മനസിലാക്കുക. 5 + 6 എന്നത് കമ്പ്യൂട്ടര്‍ മനസിലാക്കുന്നത് 101 + 110 (ഒന്ന്,പൂജ്യം,ഒന്ന് + ഒന്ന്,ഒന്ന്,പൂജ്യം) എന്നായിരിക്കും. ബൈനറി സംഖ്യകള്‍ കൂട്ടുമ്പോള്‍: 0+0=0, 1+0=1, 0+1=1, 1+1=10 (ശിഷ്ടം:1) എന്നിങ്ങനെയാവും നമുക്ക് ഉത്തരം ലഭിക്കുക. അതായത് 101+110=1011 എന്ന് കമ്പ്യൂട്ടര്‍ കണക്കുകൂട്ടും, എന്നിട്ടതിന്റെ ഡസിമല്‍ രൂപം നമുക്ക് ഉത്തരമായി ലഭ്യമാക്കും. 1011 ന്റെ ഡസിമല്‍ എന്നു പറയുന്നത്: 1*(2^3)+0*(2^2)+1*(2^1)+1*(2^0)=11 എന്നു ലഭിക്കും.
--
'എന്തും ഏതും' പുതിയ നിര്‍‌വചനം - എനിക്കറിയാവുന്നത്!
sOrry hari..may be hariyude ee blogile ente moonnamathe comment aakanam ithu .
Parayathirikkan vayya.. Njaan harmony nashippichu ennu :) ha ha ha ha... A harmony sukhichondirunna aalaanu ee sahyan alle?
Sahyanu olippeeru kavitha polum vashamilla.. paavam..
(Commentaan vendi maathram ulla id?)
Once again sorry hariyey..
ആലപ്പുഴക്കാരന്‍ വിഷ്‌, എഴുതുന്നവര്‍ മാത്രേ കമന്‍റാന്‍ പാടൂ എന്നാരാ തന്നെ പഠിപ്പിച്ചത്‌? എന്താണ് ഒലിപ്പീര് കമന്‍റെന്നും കവിതകളെന്നും സഹ്യനെ ആരും പഠിപ്പിക്കേണ്ട, തന്നെപ്പോലുള്ള അനാവശ്യ പുറം ചൊറിയലുകാരാണ് ബ്ലോഗിങ്ങിന്‍റെ ശാപം. ഇവിടത്തെ റ്റാഗില്‍ പറഞ്ഞതും ഉള്ളടക്കവും വായിക്കാദ്യം എന്നിട്ടുമതി സഹ്യനെപറ്റി പറയല്‍ തന്നെപ്പോലുള്ള വിവരദോഷികള്‍ക്ക്‌ ഈ പോസ്റ്റിലെഴുതിയതെല്ലാം 'ടെക്കനോളജി' യായിതോന്നും എല്ലാവരും താനല്ലല്ലോ - യേത് ;)
Post a Comment
40- ദിവസത്തിനു മേല്‍ പ്രായമുള്ള പോസ്റ്റുകളുടെ കമന്റുകള്‍ പരിശോധിച്ചതിനു ശേഷം മാത്രമേ പ്രസിദ്ധീകരിക്കുകയുള്ളൂ. സഹകരിക്കുക.
--